Increasing Importance of demand forecasting

In our recent research, Supply Chain Planning in The Cloud, SAPinsiders highlighted that demand forecasting remains a key challenge. Fortunately, best-of-breed supply chain tools today provide many features and functionalities, including a rich portfolio of algorithms, that can help bring more science and certainty into this exercise. However, as the popular saying of "Garbage-In-Garbage-Out (GIGO)" goes in the world of analytics, a significant portion of the quality of your forecasts is also dependent on data preprocessing. And best-of-breed solutions help users in this area as well. This article will explore the important pre-processing step of outlier detection and the associated algorithms available to users when working on demand forecasting leveraging SAP IBP.

Outlier Detection Feature for Demand Forecasting in SAP IBP

In simple terms, pre-processing allows you to improve the quality of your data. This step eliminates noise factors in your data that may impact the quality of the forecast. To simplify it further, this "noise" is data discrepancies that may confuse the algorithm or make it interpret the data in abnormal ways. Common examples are large value outliers, a significant percentage of missing values, any lifts from marketing promotions, etc. Let us explore SAP IBP's tools to help address outliers in your data.

Data Outliers

There are a couple of ways IBP can help you address outliers in your dataset:

• Interquartile range test
• Variance test

Interquartile range test: This algorithm allows you to substitute missing values through mean, median or tolerance values. The algorithm identifies the outliers and then substitutes them with the average values in the normal range. This algorithm uses the first and third quartiles in threshold calculations, leveraging the statistical method of Box and Whiskers plot. The formula that the algorithm uses to identify the outliers is: Inter Quartile range = Quartile 3 – Quartile 1 The second quartile cuts the data into two equal parts (the median or the 50th percentile). The third quartile splits the highest 25% from the lowest 75% (the 75th percentile). The figure below illustrates the quartile ranges for normal distribution.

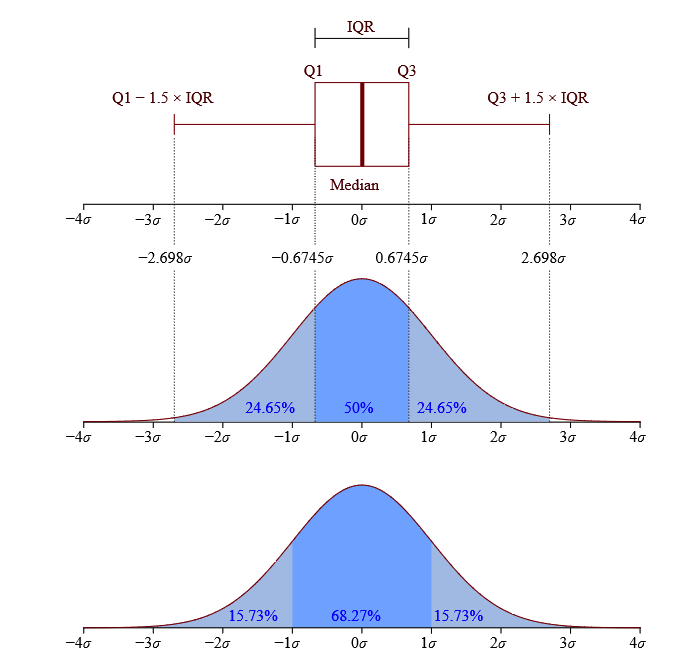
Source: Statistics.com

Upper threshold = Quartile 3 + (Multiplier * IQR) Lower threshold = Quartile 1 – (Multiplier * IQR) The multiplier is the number of standard deviations. The algorithm considers any value that lies outside these threshold points an outlier. Users can exclude or consider these outliers during the substitution calculations. Outliers can be substituted with the following values:

• Mean
• Median
• Tolerance values
• Tolerance excluding outliers

The interquartile range test is SAP's method of choice for outlier correction. Variance test: The variance test algorithm is relatively simpler but is considered relatively less flexible in data sets that are more volatile since it leverages mean as the core benchmark in its calculations. The thresholds for this test are defined as below:

• Lower threshold = Mean – Multiplier × standard deviation
• Upper threshold = Mean + Multiplier × standard deviation

Any values that fall outside this range are considered outliers. These outliers can then be substituted similarly to the IQR method.