Karsten Bohlmann's follow-up to part 1 of his series on ABAP focuses on those 7.40 additions to the ABAP programming language that deal with internal tables, covering table access as well as table construction, aggregation, grouping, and transformation. Most of the extensions aim at a mitigation of the strict imperative paradigm.
Key Concept
ABAP is a typical procedural language with object orientation as an optional refinement. More modern languages recognize the fact that many programming tasks can be conceived as pure value computations which have concise, lucid implementations as expressions.
If you liked what you saw in
part 1 of this survey of 7.40 ABAP language features, you’ll surely enjoy the second half. It’s all about internal tables—the flexible and powerful collection mechanism so fundamental to ABAP that the language would be quite useless without it.
Unfortunately, ABAP constructs to build and access internal tables have so far been on the evolutionary stage of "MOVE x TO y" and "COMPUTE X = y + 1," statements that I made some fun of in part 1: They are redundant, non-orthogonal, and force us to think in terms of micro-effects on state instead of recipes for building values from other values, which would be the appropriate view for a big share of programming tasks.
For tables, you are confronted with statements like these:
READ TABLE tab WITH KEY c1 = 'a' ASSIGNING <line>.
LOOP AT tab1 ASSIGNING <line> WHERE c1 = 'a'.
INSERT <line>-c2 INTO TABLE tab2.
ENDLOOP.
Remember how jobs such as type conversion and structured-value construction were relieved from imperative misery by constructor expressions:
use_string( CONV string( char10 ) ).
use_struct( VALUE t_struc( c1 = 'a' c2 = 10 ) ).
This was supported by the anti-redundancy concepts of inline declaration and type inference, from which table statements can profit already:
READ TABLE tab INDEX 1 ASSIGNING FIELD-SYMBOL(<line>).
INSERT VALUE #( c1 = 'a' c2 = 10 ) INTO TABLE tab.
And it’s already known how to construct tables with a fixed number of lines as values:
use_inttab( VALUE #( ( x - 1 ) ( x ) ( x + 1 ) ) ).
There are two main gaps to close:
- Access table lines without a state-manipulating statement like READ.
- Construct table values with a variable number of lines (e.g., from lines of another table).
After these, I proceed to more challenging tasks, like reducing a table to a non-table value, processing table lines in groups (think of SQL’s GROUP BY), and performing the good old MOVE-CORRESPONDING operation on tables, with user-defined mappings.
Table Line Selection
Obviously, only a single choice of syntax for table access exists that will not leave 90 percent of programmers bewildered: square brackets. To access the first line of a table, we expect to write
tab[ 1 ]
And yes, that’s the new ABAP syntax for "READ TABLE tab INDEX 1".
This new kind of expression works at all “expression-enabled” positions of the ABAP grammar (which boils down to read operands of non-obsolete, non-peripheral statements). But the selected table line is also an l-value, comparable in this respect to the NEW and CAST expressions known from part 1:
tab[ 1 ] = struc.
tab[ 2 ]-c1 = 'a'.
The first line is an assignment that changes a table line as a whole, while the second line shows the (more frequent) case that only one component of the line is modified, by chaining the table selection with the component selector "–".
Two selection methods are available inside "[…]": by index or by component value(s). The latter has the form:
tab[ c1 = x c2 = f( y ) ]
If several lines match the search, which line you get is defined by the order of line insertion (same as for READ). Both variants may refer to an explicit key defined for the table type:
tab[ KEY key1 INDEX 1 ]
tab[ KEY key1 c1 = x c2 = f( y ) ]
A (primary or secondary) key used for index access must not be a hash key. Components of an explicit key must be matched, like in the "READ TABLE … WITH TABLE KEY" statement. Otherwise, the expression has the free-key semantics of "READ TABLE … WITH KEY" which implicitly uses the primary key if possible. Components, as well as the key name, can be dynamic:
tab[ KEY (keyname) c1 = x (compname) = y ]
So there are functional equivalents for most flavors of the READ statement. (The "FROM workarea" and "BINARY SEARCH" variants are not supported.)
A natural question for an ABAP developer to ask is now: “Is this a READ … INTO or a READ … ASSIGNING (i.e., do I get a copy of the line or a pointer to it)?” The answer is: Usually you don’t have to bother; the compiler takes care of it by considering the context and the line type:
- Certain contexts (such as method call, see below) mandate pointer semantics.
- Also, if the line type is generic, a pointer is the only option.
- If the line type is “wide” or “deep,” the compiler chooses pointer semantics because it is more efficient. If the type is “narrow” and “flat,” you get copy semantics. This optimization is applicable in most r-value positions.
In a method call, the compiler uses pointer semantics by default. (Copy semantics as a tacit optimization could lead to different behavior due to side effects.) However, if the line type is narrow and flat, the Extended Syntax Check (SLIN) issues a warning to “consider VALUE selection.” This hints at the following syntax variant:
VALUE #( tab[ … ] )
It tells the table selection to copy the line out of the table into a separate value. Usually it’s a good idea to follow that SLIN hint. An analogous variant
REF #( tab[ … ] )
obtains a reference to the line, to be used (e.g., when a REF TO linetype parameter is required).
So these are new inner syntaxes for the VALUE and REF operators from part 1 of this series. There is no extra operator for ASSIGNING; it is the default. But how to assign a table line explicitly to a field-symbol, possibly combined with an inline declaration? Like this:
ASSIGN tab[ i ] TO FIELD-SYMBOL(<line>).
Above, there was already an example of component chaining. It generalizes to data structures with tables nested at arbitrary depth. For “table of tables” types, chaining looks like multidimensional array access:
ASSIGN matrix[ x ][ y ] TO <point>.
Otherwise, the chain includes a dash and the component name ("-tab1", "-c3"):
tab0[ x ]-tab1[ c1 = y c2 = z ]-c3
Note the syntactic similarity with method call chaining:
meth0( x )->meth1( p1 = y p2 = z )->a
A table selection can be followed, but not preceded by a method call (this discourages inefficient designs, which retrieve a whole table by method call only to extract one line):
t1[ x ]-reftab[ y ]->meth( )
t2[ x ][ y ]-ref->meth( )->a
"meth( )[ x ] " not allowed, syntax error
Chaining examples illustrate well how lengthy imperative code, riddled with helper variables, can be shrunk:
READ TABLE t1 INDEX x ASSIGNING FIELD-SYMBOL(<x>). " *yawn*
READ TABLE <x>-reftab INDEX y INTO DATA(ref). " zzzz…
ref->meth( ).
But what if a selection fails? Clearly this is not a situation to be signaled by some error code in SY-SUBRC. Side effects from expressions are distasteful; expression constructs never change SY fields. Instead, a failing table selection throws an exception of class CX_SY_ITAB_LINE_NOT_FOUND. The exception object contains information about what failed (e.g., which index). Sometimes, but not always, that allows you to tell which selection in a chain failed. If you need more control, you have to split the chain. For example:
ASSIGN t2[ x ] TO FIELD-SYMBOL(<x>).
CHECK sy-subrc = 0.
ASSIGN <x>[ y ] TO FIELD-SYMBOL(<y>).
Unlike expression-level selections, the ASSIGN statement, in its own tradition, sets SY-SUBRC to 0 (“success”) or 4 (“failure”), which can be reacted to in control flow.
If non-existence of a searched line is an expectable case for which you have a default value, the VALUE operator comes to the aid again:
VALUE #( tab[ x ][ y ] DEFAULT deflt )
This yields the value of deflt if any of the chained selections fails. To obtain the initial value in this case, write:
VALUE #( tab[ x ][ y ] OPTIONAL )
There is a built-in predicate function to test mere existence of a line:
CHECK line_exists( tab[ c1 = x ] ).
Or if you need the index of the found line:
DATA(i) = line_index( tab[ c1 = x ] ).
If no line is found, this returns 0. Both functions also work for chained selections—then the result refers to the final selection in the chain. Neither of them ever throws an exception.
Caveat: The convenience of expressions is seductive. When operations can be written with so little typing effort, something like this may slip out:
tab1[ idx1 ]-a = tab2[ idx2 ]-x.
tab1[ idx1 ]-b = tab2[ idx2 ]-y.
tab1[ idx1 ]-c = tab2[ idx2 ]-z.
Unfortunately, the ABAP compiler is still very weak at optimization; for example, it doesn’t perform common sub-expression elimination. So you have to factor out intermediate results yourself or you will be punished by bad run time. In this example, reduce six table selections to the necessary two:
ASSIGN tab1[ idx1 ] TO FIELD-SYMBOL(<r1>).
ASSIGN tab2[ idx2 ] TO FIELD-SYMBOL(<r2>).
<r1>-a = <r2>-x. <r1>-b = <r2>-y. <r1>-c = <r2>-z.
Table Comprehension
No more questions about table line access? So the next challenge is to construct tables as values, without resorting to the “many little state-manipulations” idiom:
LOOP AT tab ASSIGNING FIELD-SYMBOL(<x>) WHERE c0 = 'X'.
INSERT VALUE #( d1 = <x>-c1 d2 = <x>-c2 )
INTO TABLE tab1.
ENDLOOP.
The wanted concept is long known and has its formal roots in mathematical set notation:
{
f (
x) |
x Î
S,
P(
x) }
Is the set of values
f (
x) computed by result function
f for all those elements
x from the source set
S for which predicate
P(
x) is true. When applied to the list container (popularized in many functional languages, e.g., Haskell), this is called list comprehension. In ABAP, the container concept is the internal table, so the name is adjusted in the obvious way. Syntactically, the result expression
f (
x) moves to the end. This way, table comprehension emerges as a smooth generalization of table construction with the VALUE operator (
Figure 1).

Figure 1
Anatomy of a table comprehension
- The FOR clause introduces the “expression-level LOOP”; it binds either a local field-symbol (something named "<…>") for “LOOP ASSIGNING” semantics, or a local variable for “LOOP INTO” semantics. As explained in part 1, such a local variable may be re-used in other expressions, but not on statement level. The worlds of local and non-local variables must be kept distinct.
- The expression after IN specifies the source table, lines of which are bound to the FOR symbol in turn.
- Optionally, the visited lines can be restricted to a subset:
- A FROM /TO clause specifies the index range in the source table.
- A WHERE clause filters lines by a logical expression. (Parentheses around the logical expression are necessary to avoid parsing problems.)
- A USING KEY clause (not shown here) may precede both to specify the table key to be used for these restrictions.
- The LET clause for binding local variables has already been seen in part 1. In a table comprehension, it typically serves to avoid multiple computations of a value derived from the current line (referenced by the FOR symbol). Note in the example of Figure 1 how a table selection (l-value!) is bound to a local field-symbol (not variable), thus avoiding copy semantics for the table lookup.
- Finally, one or several line specifications follow, as in the static case, but using the FOR symbol.
In accordance with the “no side effects” principle, a FOR loop does not set SY-TABIX. If you need the current-line index, you can bind a local integer variable in a clause after FOR:
VALUE #( FOR x IN tab
INDEX INTO i
( idx = i val = x ) )
A comprehension can have more than one FOR clause. Such nested loops are useful for flattening a hierarchical structure (second FOR iterates over a table contained in current line of first FOR), or for building the cross-product of two tables (independent FOR loops):
VALUE #( FOR <x> IN tab1
FOR <y> IN tab2
( d1 = <x>-a d2 = <y>-b ) )
However, you cannot have a FOR clause after a result line specification. This excludes certain kinds of flattening, which may be possible with REDUCE though (see below).
Instead of a source table, you can use a range of values, specified by a start value, an increment expression, and an end condition:
VALUE #( FOR k = 1 THEN k + 2 UNTIL k > 9
( k * k ) )
Yields the table of odd squares [1, 9, 25, 49, 81]. The THEN clause may be absent if the iteration variable is numeric; then the default is to increment it by 1. Use WHILE (and a negated end condition) instead of UNTIL if the range is possibly empty: UNTIL is checked after each iteration and WHILE is checked before—that’s the only difference.
[ i*i | i <- [1,3..9] ]
Granted, this is even shorter, but as you probably agree, no longer ABAP-esque.
In more general terms, table comprehension allows you to apply a function to all elements of a collection, thus obtaining a new collection (whose element type is the function’s co-domain). This is the description of the higher-order function
Map. Very often it goes hand in hand with closures (anonymous functions as values), which are not currently available in ABAP. If they were you’d write something like:
Map( f strtab ) with the mapping function defined as
f(s) = strlen( s )
To apply function m to a table strtab of strings, obtaining a table of integers. What we actually have is a bit less abstract:
VALUE #( FOR s IN strtab ( strlen( s ) ) )
Basically it just lacks the ability to pass the function as a parameter into the
Map from outside.
Table Reduction
The best friend of
Map is the
Reduce functional. Comparing their signatures (
Figure 2), shows that
Reduce, unlike
Map, reduces table nesting. It transforms a table of elements of type S to a single value of type T. To do so, it requires a binary operator to combine a pair of T and S into T, and a start value of type T. For example, to compute the sum of string lengths, use
Reduce like this (in hypothetical syntax again):
Reduce( g 0 strtab ) with the reducing operator defined as
g(t,s) = t + strlen( s )
which evaluates to
0 + strlen( strtab[ 1 ] ) + strlen( strtab[ 2 ] ) + …
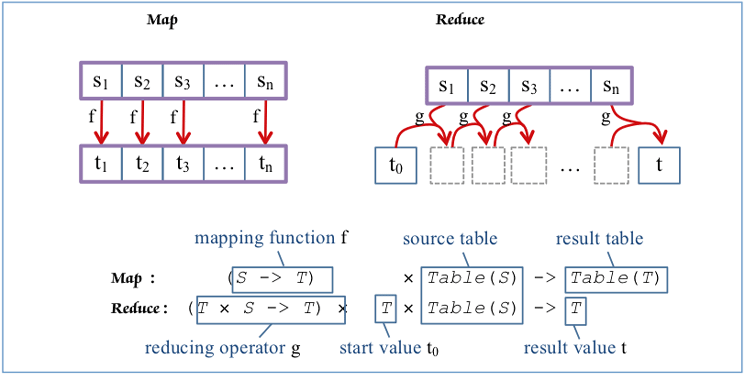
Figure 2
Higher-order functions Map and Reduce underlying table comprehension/REDUCE
In actual 7.40 ABAP syntax, REDUCE is yet another constructor operator, very similar to a table comprehension VALUE, also with FOR as the central clause.
REDUCE #( INIT t = 0
FOR s IN strtab
NEXT t = t + strlen( s ) )
Here is an operational explanation of how it works: The INIT clause defines a local “accumulator” variable with a start value. The NEXT clause is evaluated as many times as scheduled by the FOR clause and defines the accumulator’s next value (typically using its previous value and the iteration variable). It’s an easy exercise to find the elements of Reduce in this description.
If required, further (auxiliary) variables can be defined in the INIT section and must then be re-computed in the NEXT section. This simple example concatenates values into a string, setting the “separator” variable only after the first value (to insert commas between values):
REDUCE #( INIT str = `Values: `
sep = ``
FOR <x> IN tab
NEXT str = str && sep && <x>
sep = `, ` )
Type inference may flow in both directions: Either the context prescribes a type for the REDUCE expression, or its type is inferred from the INIT expression. In INIT, you may also use a type declaration; then the start value is the type’s initial value. Here, INIT i = 0 could be replaced with INIT i TYPE i.
REDUCE doesn’t necessarily lead to a reduction in complexity with respect to the type of the source collection. To see this, consider the following alternative way of building the table of odd squares (clumsy, not recommended):
REDUCE #( INIT t = VALUE #( )
FOR k = 1 THEN k + 2 UNTIL k > 9
NEXT t = VALUE #( BASE t ( k * k ) ) )
Here, the BASE addition of VALUE is used to build the table incrementally in the accumulator variable.
To compute more than one reduced value in one sweep, one needs a suitable structure type because ABAP doesn’t have “ad-hoc tuples.” For instance, to find the minimum and maximum of a table, with a pair of integers type for the result:
REDUCE #( INIT r = VALUE #( min = cl_abap_math=>max_int4
max = cl_abap_math=>min_int4 )
FOR <x> IN tab
NEXT r-min = nmin( val1 = r-min val2 = <x> )
r-max = nmax( val1 = r-max val2 = <x> ) )
As you see, structured accumulator variables in NEXT can be computed not only as a whole, but also component wise.
A nice REDUCE pattern emerges with a fluent interface, i.e., a set of methods whose return value is the object of the invocation (or at least the same object type):
DATA(out) = REDUCE #( INIT o = cl_demo_output=>new( )
FOR k = 1 UNTIL k > 5
NEXT o = o->write( k ) ).
out->display( ).
Here the cl_demo_output object moves through the iterations via "NEXT o = o->…".
Grouping
Everything presented so far could be tagged as “just syntactic sugar.” Your programs can gain a lot of conciseness and elegance from these functional constructs, but at the end of the day, the compiler generates largely the same byte code as for the equivalent program in plain old imperative style. The source code is shorter, but the run time is the same.
The next feature is a bit different. It is even harder to emulate with traditional statements, in some cases impossible without loss of performance, and it is a very powerful tool for processing data in internal tables in non-trivial ways.
To begin with, think of the SQL GROUP BY clause. Maybe you also know the SQL:2003 extension of “window functions,” which addresses certain weaknesses of GROUP BY. ABAP 7.40 introduces a similar mechanism for internal tables. The following review focuses on its statement form (an extension of LOOP), but there is also an expression form.
Figure 3 shows the basic structure of a LOOP … GROUP BY statement. It starts out like a normal LOOP, specifying a source table, possibly FROM/TO/WHERE clauses to restrict the set of visited lines, and most notably the binding of an iteration symbol via ASSIGNING or [REFERENCE] INTO. This symbol is used in the GROUP BY clause to compute, for each visited line, its group-key value (gkv). Any kind of expression is allowed here, not just a column name of the source table (that’s why the iteration symbol is required). All lines with the same gkv end up in one group. The loop body is executed once for each group, with the iteration symbol bound to a representative line for the group. The representative is the first (according to the well-defined LOOP order) line of the group.
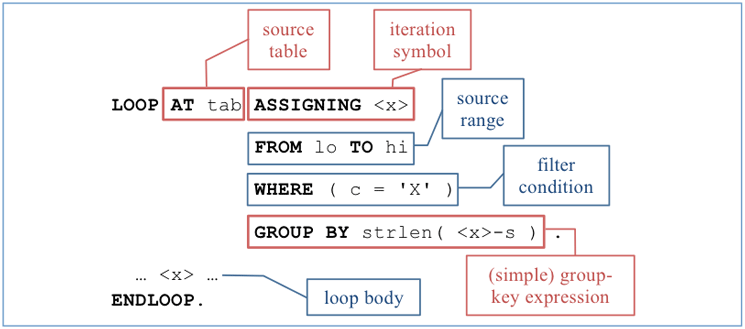
Figure 3
Grouping loop (simple group-key expression, no group-symbol binding)
The loop body in
Figure 3 might use the group representative in <x> as follows:
WRITE / |Length: { strlen( <x>-s ) } String: { <x>-s }|.
That would output a line for each distinct string-length value, with a representative string.
But there is something unsatisfactory about this example: The expression to compute the gkv is needed again in the loop body; it must be re-written and re-computed there. This weakness is known from SQL which, although it avoids re-computation at run time, does require you to repeat the exact same expression of the GROUP BY clause in the SELECT clause.
In ABAP, you can do better, by providing a binding for the gkv after the GROUP BY clause. Like the iteration symbol for the source table, it can use INTO or ASSIGNING, and inline declaration. Instead of visiting group representatives in <x>, this variant gives the loop body access to the gkv in the group symbol (here: slen):
LOOP AT tab ASSIGNING <x>
GROUP BY strlen( <x>-s ) INTO slen.
WRITE / |Length: { slen }|.
ENDLOOP.
Fine—now the grouping expression is neither repeated nor re-computed. But we don’t have access to a group representative anymore. An attempt to access <x> in the loop body would find it unassigned.
The remedy is a mechanism that gives access to all group members: Within the (statically nested) body of a grouping loop, the “member loop” statement LOOP AT GROUP, which references the provided group symbol, iterates over the members of the current group:
LOOP AT tab ASSIGNING <x>
GROUP BY strlen( <x>-s ) INTO slen.
WRITE / |Length: { slen }|.
LOOP AT GROUP slen ASSIGNING <x>. " member loop
WRITE / | String: { <x>-s }|.
ENDLOOP.
ENDLOOP.
This outputs each distinct string-length value, followed by all strings of that length.
Header-items patterns like this are quite common. In addition, one often wants to have the groups ordered by the gkv, instead of by the order of discovery. No problem—simply add ASCENDING or DESCENDING after the GROUP BY clause:
LOOP AT … GROUP BY strlen( <x>-s ) ASCENDING INTO slen.
This orders groups by ascending string-length value.
The LOOP AT GROUP statement may have its own WHERE clause and what’s more, it can have another GROUP BY, which gives you multi-level grouping. For example, first by initial letter and then by length:
LOOP AT tab ASSIGNING <x>
GROUP BY substring( val = <x>-s len = 1 ) INTO char.
WRITE / |Letter: { char }|.
LOOP AT GROUP char ASSIGNING <x>
GROUP BY strlen( <x>-s ) INTO slen.
WRITE / |Length: { slen }|.
LOOP AT GROUP slen ASSIGNING <x>.
However, a simple case like this, without further intermediary logic between the two nested GROUP BY loops, can be optimized into a single loop, using a gkv tuple. Let’s group by initial letter and length simultaneously:
LOOP AT tab ASSIGNING <x>
GROUP BY ( char = substring( val = <x>-s len = 1 )
slen = strlen( <x>-s ) )
ASCENDING ASSIGNING FIELD-SYMBOL(<g>).
WRITE / |Letter: { <g>-char } Length: { <g>-slen }|.
The compiler provides the required structure type (with components char and slen in this case) automatically. But remember, you don’t need parentheses for a single gkv expression:
… GROUP BY ( key = expr ) … " useless 1-tuple
This would unnecessarily induce a single-component structure type.
There is no extra support for SQL-like aggregate functions, since aggregations are easy to do inside the loop (e.g., by a REDUCE). Conditions can be checked inside the loop as well, so there is no need for a HAVING clause either:
LOOP AT … GROUP BY … ASSIGNING <g>.
DATA(groupsum) = " an aggregation
REDUCE i( INIT u = 0 FOR m IN GROUP <g>
NEXT u = u + m-val ).
" a 'HAVING condition'
CHECK groupsum > 100.
Oops, that was already an example of a member loop in a REDUCE expression. On the expression level, variable binding moves to the front, so the grouping loop:
LOOP AT
Source GROUP BY
GrpExpr ASSIGNING <g>
becomes:
FOR GROUPS <g> OF
Source GROUP BY
GrpExpr
Here is a usage of a grouping expression to eliminate duplicates from a table:
VALUE #( FOR GROUPS OF <x> IN tab GROUP BY <x> ( <x> ) )
Of course you can use any other criterion of equality, including a tuple-shaped gkv.
Finally, here is a little test for your spiritual progress on the functional path—an expression to compute the maximum of group averages:
REDUCE decfloat34( INIT max = 0
FOR GROUPS <g> OF <x> IN tab
GROUP BY ( k = <x>-key size = GROUP SIZE )
LET gsum = REDUCE #( INIT s = 0
FOR <m> IN GROUP <g>
NEXT s = s + <m>-val )
gavg = CONV decfloat34( gsum / <g>-size ) IN
NEXT max = nmax( val1 = max val2 = gavg ) )
The pseudo-group key component GROUP SIZE is used to receive the size (number of members) of a group. You need it here to compute the group average.
One caveat at the end: During a GROUP BY loop, the table must not be modified, because the implementation uses line indices that might be invalidated otherwise. A modification attempt leads to a run-time error. (Exception: Insertion into a hash-table; it doesn’t hurt indices.) But if you don’t need access to group members, you can add a clause that says so: GROUP BY … WITHOUT MEMBERS. It has three implications:
- The loop gets a bit faster because group membership of lines is not recorded.
- You don’t have access to table lines, but only to the group key value.
- You can modify the table during the loop.
Table and Structure Mapping
Typical ABAP applications abound with large structure types. Structure inclusion and field extension are key mechanisms to build (e.g., “joins” and “projections”) situations in which an object-oriented (OO) approach would likely use inheritance. As a result, ABAP developers often face a pair of somehow “similar” data types and the task to transform one into the other. ABAP’s MOVE-CORRESPONDING statement is tailored to this job: It maps structure components by name matching, regardless of position. Due to internal optimization (bulk handling of consecutive components) it is often faster than a sequence of single MOVEs. This power has earned the statement great popularity. Savvy ABAPers even use type-casting to impose “views” on data such that they are amenable to MOVE-CORRESPONDING. In 7.40 the statement’s power has been further increased, and some of these tricks involving type casts are no longer necessary.
Consider the four cases in
Figure 4. For simplicity, assume all leaf components have the same type (e.g., CHAR10). Previously, the “corresponding names” logic was limited to structures. Structure nesting was no problem; for example, in case (i) the sub-components of b were mapped correctly. But in case (ii), where b is a table component, it would be subjected to a structure-agnostic MOVE, resulting in swapped components b1 and b2 (or error, if they weren’t compatible.) Cases (iii) and (iv) were forbidden altogether.

Figure 4
Possible applications of [MOVE-]CORRESPONDING
These restrictions are now lifted. The desired behavior in (ii) and (iv) is achieved by an addition that extends name-matching to the components of the nested table:
MOVE-CORRESPONDING src TO dst EXPANDING NESTED TABLES.
Case (iii) works even without this addition.
A statement-less solution is provided by a new constructor operator:
CORRESPONDING t_dst( src )
This also confines name-matching to the top level. The equivalent of the “EXPANDING NESTED TABLES” clause is simply called DEEP. For example, the desired mapping in case (iv) is achieved by:
CORRESPONDING #( DEEP src )
Like the VALUE operator, CORRESPONDING builds its result from scratch. It matches the source value src against the destination type t_dst, taking no destination value into account. But, like VALUE, it has an optional BASE clause to specify a start value of destination type. The effect of the statement could be mimicked in this manner:
dst = CORRESPONDING #( BASE (dst ) src ). " case (i)
dst = CORRESPONDING #( DEEP BASE (dst ) src ). " case (ii)
BASE is also applicable in (iii) and (iv); then it preserves the existing lines in table dst instead of starting from an empty table. The statement variant has a clause “KEEPING TARGET LINES” for the same purpose.
So far, there could be really annoying situations in which MOVE-CORRESPONDING was “almost” applicable: In
Figure 4, source component x might have destination y, but name matching doesn’t pair them up. Or the opposite: Components named a1 match but they have a different meaning and should not be mapped. You would either have to fix such differences in some post-processing code, or solve it without using MOVE-CORRESPONDING at all.
The CORRESPONDING operator deals with these problems smoothly. In order to map x to y and leave a1 alone, simply write:
CORRESPONDING #( src MAPPING y = x EXCEPT a1 )
There can be any number of equations after MAPPING and destination components after EXCEPT. Mapping one source component to several destination components is okay, but not vice versa. To deal with components in nested tables, you descend into the type structure within “( … )”. That is, if b1 should receive the value from b2 and b2 should remain initial:
CORRESPONDING #( src
MAPPING y = x ( b = b MAPPING b1 = b2 EXCEPT b2 )
EXCEPT a1 )
The feature does have its limitations: You cannot jump across type levels in mappings, nor can you mix in data from anywhere else but the source structure. Things like that typically require a table comprehension. But if a solution with CORRESPONDING exists, it is usually faster because it is an “atomic” operation for the ABAP virtual machine.
A special variant for internal tables supports the lookup of additional data in another table:
CORRESPONDING #( dst FROM dir USING id = a1 MAPPING y = z )
Assuming that the “directory table” dir has a key column ID and further component z, this expression augments each line of table dst by looking up the value of a1 in dir, and moving the value of z from the found line to y. Components used for lookup are not moved. Lines with unsuccessful lookup appear un-augmented in the result (“left outer join”).
Let’s conclude the tour of powerful table operations with the FILTER operator. It implements a different kind of lookup—instead of “augmenting” lines, it eliminates lines:
- Filtering by values:
FILTER #( src WHERE a1 = 1 AND a2 > 0 )
yields those lines of table src which fulfill the conditions after WHERE (using =, < and related comparison operators, all conditions linked by AND). Conversely,
FILTER #( src EXCEPT WHERE a1 = 1 AND a2 > 0 )
yields the lines not fulfilling the condition.
- Filtering by lookup table:
FILTER #( src IN dir WHERE id = a1 )
yields those lines of table src for which an entry in table dir exists that fulfills the condition (i.e. <dir>-id1 = <src>-a1), so this is a kind of generalized set intersection operation. Conversely,
FILTER #( src EXCEPT IN dir WHERE id = a1 )
yields the lines for which no such entry exists, making it a kind of generalized set difference.
The operation must be supported by a key on the inspected components of table src in case a, and table dir in case b. The key may be specified (USING KEY k) before WHERE. Again, table comprehension can do the job as well, but the specialized operator, when applicable, is usually more efficient.
Conclusion
In this second part of the 7.40 ABAP survey you have learned many new ways of working with ABAP’s internal tables in a 21st-century style. These features may not be applicable “in every other line of code,” like some of the stuff presented in part 1, but still they come in handy very often, because internal tables are so ubiquitous.
Accessing table lines by “[…]” expressions was surely straightforward. Hopefully I could also convince you that the task of building an entire table from another (or from a range of values) is not one that requires a lame statement sequence. Isn’t it much more uplifting to look at it as an application of the higher-order “Map” function? Or to reduce a table to a single value by the operator of the same name?
Certain other tasks don’t need the generality of table comprehension because they can be solved efficiently by specialized operators CORRESPONDING or FILTER. And when confronted with a complex aggregation-type problem, you should check if it’s a case for a GROUP BY loop.
So, when equipped with a 7.40 system, go ahead—write ABAP code that "doesn’t look like ABAP” any more.
Karsten Bohlmann
Karsten Bohlmann is currently a development architect in the ABAP language team. He has been an SAP employee since 1998 and joined kernel development in 2000, where he developed the kernel-integrated XSLT processor and the Simple Transformations language for ABAP-XML mappings. Since 2005, he has been active in the ABAP compiler and virtual machine, spending most of his time on expanding ABAP towards a more modern language.
You may contact the author at
karsten.bohlmann@sap.com.
If you have comments about this article or publication, or would like to submit an article idea, please contact the
editor.










